StarkEffects.com
Articles by Subject Category
Physics Basics Series
- Basics of Classical Mechanics.
- Basics of Quantum Mechanics.
- Basics of Electrodynamics.
- Basics of Optics.
- Basics of Mathematical Tools for Physics.
- Basics of Plasma Physics.
- Basics of Solid State Physics.
Troy Stark's Science & Society Opinion Blog
Concise Articles, Tutorials & Primers on Physics, Math & Technology & Obscure Science Topics
Welcome to StarkEffects.com page on the Taylor Series Expansion!
A short description of the Taylor Series, how it is derived and how to use it.
A Derviation of the Taylor Series Expansion
An often-used polynomial expansion is the Taylor series. Approximating the value of a complicated function is a very useful technique. The Taylor series expansion serves as a workhorse in many computer programs to approximate functions that would otherwise be very difficult to program. In other words, the programmers (or their technical advisors) did their algebra first, before writing the program in order to make the program run faster or maybe even make it possible.
A Look at How This Expansion is Derived
Series expansions are an excellent way to quickly represent a complicated function as a simple power series. One reason for doing this is to allow a quick, approximate evaluation of the function at given points or to allow a computer algorithm to approximate a function with more speed than it could attain if it were to actually evaluate the function during a process. With that introduction, let’s look at how we derive a Taylor series expansion for a given function.
Suppose you have a function, 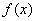 , defined for a range of
, defined for a range of 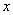 values. We would like an approximation for quickly evaluating
values. We would like an approximation for quickly evaluating 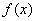 , that looks like a simple polynomial with increasing powers of
, that looks like a simple polynomial with increasing powers of 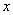 .
.
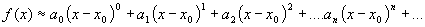
As you can see, the expression would be easy to evaluate, since you only need to get the value  one time and if you know the coefficients in front of each power of this term you have it made. Of course, there is the little complication that this series expansion goes on forever, but that is taken care of in many cases by each successive term becoming smaller and smaller so that you have a very good approximation of the value of
one time and if you know the coefficients in front of each power of this term you have it made. Of course, there is the little complication that this series expansion goes on forever, but that is taken care of in many cases by each successive term becoming smaller and smaller so that you have a very good approximation of the value of 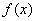 after just a few terms. It helps if
after just a few terms. It helps if 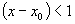 so that each successive power is smaller and smaller. Note however, that even if this is the case, the nature of
so that each successive power is smaller and smaller. Note however, that even if this is the case, the nature of 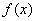 still determines if you will “converge” to a good approximation after a few terms of the polynomial.
still determines if you will “converge” to a good approximation after a few terms of the polynomial.
Let’s proceed anyway and derive a general solution that we can use in the many cases of functions that will produce a polynomial that converges quickly to a good approximation of the function. We start by evaluating our function at 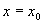 which gives us:
which gives us:

This is the only term left in our series expansion since  for all
for all 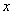 including
including 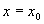 while all of the other terms go to
while all of the other terms go to  for
for 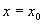 . So we have:
. So we have:
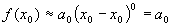
Now we have the first coefficient in our series expansion. It is the value of our function at a point that we know the value.
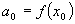
Now we need a way to get the next coefficient and it needs to be a way that eliminates all of the later coefficients in a similar manner to the way we just did for the first one (the zero order coefficient). It just so happens that taking the first derivative of our equation does exactly what we need:
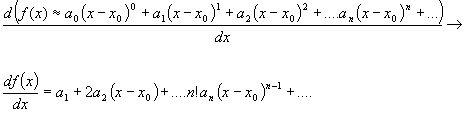
If we evaluate this function at 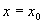 we quickly get:
we quickly get:

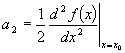

Which allows us to write:

where each coefficient is a derivative another derivative of our function evaluated at 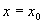

That is the Taylor series expansion of 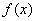 with respect to
with respect to 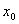 for a function of one variable. This series expansion may or may not converge depending on the function but at least now you have an expansion to work with and determine if it will provide the approximation you desire.
for a function of one variable. This series expansion may or may not converge depending on the function but at least now you have an expansion to work with and determine if it will provide the approximation you desire.
By using partial derivatives you can employ the same methods as above to find the Taylor series expansion for a function of several variables. For example, here is the result you will get for a function of three variables,  :
:
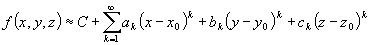
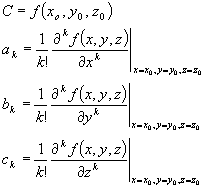
Of course, you are not limited to three variables, you can have as many as you please. The same restrictions apply to your convergence however, and now you must have convergence with respect to all of the variables in order to have a “good” approximation for your function.
Quick Science & Math References
- Our Solar System.
- Earth Facts.
- The Metric System.
- Trigonometric Identities.
- Vector & Tensor Identities.
- Explicit Forms of Vector Operators
- Light & Electromagnetic Spectrum.
- Common Laser Wavelengths.
- Human Physiology Facts.
- Human History Timeline
- Geologic Timeline
- Cambrian Explosion
- Life on Earth Timeline
- ASCII Codes and HTML Display Codes
- Thousands of HTML Symbol Codes
- HTML Symbol Codes for Greek Letters
- The Best Way to put Equations on your Web Page
Physics Basics Series
- Basics of Classical Mechanics.
- Basics of Quantum Mechanics.
- Basics of Electrodynamics.
- Basics of Optics.
- Basics of Mathematical Tools for Physics.
- Basics of Plasma Physics.
- Basics of Solid State Physics.
Math Basics Series
- Numbers
- Arithmetic
- Algebra
- Geometry
- Analysis
Technology Basics Series
- Basics of Remote Sensing.
- Basics of Digital Signal Processing.
- Critical Electronic Circuits
- Infrared Imaging Basics
Knowledge Branches
- Information Theory
- How Reading Works in the Brain
- Psychology of Learning
- Logic
WORK IN PROGRESS
- What is the Stark Effect?
- The Chemistry of Love &/or Addiction
- Critical Thinking: How to question what you see, read or hear.
- Aristotle's Prior Analytics - the birth of Logic.
- Optical Solutions, lenses that solve problems
- Fractals
- PTC - Photon Transfer Curve or Mean Variance Analysis
- 3-D Noise
- Laser Primer
- Rail Guns
- Special Relativity
- Radar Technology
- Acousto-optic Cells
- Harmonic Generation for Laser Frequency Doubling (SHG) and Tripling -using non-linear crystals.
- Measurement: Accuracy & Precision.
- Things you should know about computer modeling of physical phenomena!
- Giant Magneto-resistance
- Peltier Cooling
- Pyro-Electric Detectors
- Piezo-Electric Crystals
- Laser Speckle
- FFT and DFT the fast fourier transform and the discrete fourier transform
- Fabry Perot Etalon
- The Hydrogen Atom.
- PCA (Principal Component Analysis)
- Energy per mass in fuels such as Hydrogen, Gasoline, Kerosene, HMX etc...
- Nobel prize winning work on the CCD
- How does a CCD work and what are the normal characteristics of a CCD
- Nobel Prize Winning work on Giant Magneto-resistance
- FROG -frequency resolved optical gating
- Optical Wavefront Sensing
- THz imaging and time-domain spectroscopy
- Camera Calibration
- Laser Designators
- Resampling
