Physics Basics Series
- Basics of Classical Mechanics.
- Basics of Quantum Mechanics.
- Basics of Electrodynamics.
- Basics of Optics.
- Basics of Mathematical Tools for Physics.
- Basics of Plasma Physics.
- Basics of Solid State Physics.
Troy Stark's Science & Society Opinion Blog
Welcome to the STARKFX.com Fibonacci Numbers Page!
A quick description of the Fibonacci series and the recursive formula for it.
Fibonacci Numbers
Have you heard of Fibonacci numbers before? I know I was well past High School when I first learned of them. That should not have been, but we won’t get into a discussion of what we’re missing in public schools in this little article. Another thing we won’t discuss is the application of Fibonacci numbers to trading in the market. Apparently, that has become a big topic lately. No doubt it does have application to the complex human behavior in the stock market, but I’m not going to attempt to explain that.
History
Leonardo Fibonacci introduced the Fibonacci series in about 1200, in Italy. Leonardo of Pisa, as he is known now, grew up all over the Mediterranean. He was sent as a youngster to learn calculation from an Arab master. Leonardo actually introduced the Hindu-Arab numerals, and the methods of calculating that we are all familiar with now, to the rest of Europe. His books taught business calculation which made them more popular than the more esoteric works read by European intellectuals.
In one of his books, Liber abaci, Leonardo introduced a problem demonstrating the Fibonocci series, which is well known to mathematicians all over the world.
A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair, which from the second month on becomes productive?
The resulting sequence is: 1, 1, 2, 3, 5, 8, 13, 21, 34,
55. Each number in the sequence is
constructed simply by summing the last two numbers in the sequence. This is the first recursive number sequence
known in Europe. A French born
mathematician, Albert Girard, 1634, wrote the formula for the sequence:
Robert Simpson, 1753 at the University of Glasgow noted that the ratio of consecutive Fibonacci numbers approaches the Golden Ratio as you go higher in the sequence.
Fascination
Fibonacci numbers are the sequence resulting from starting with 1,1 and then creating the next number in the sequence by summing the last two in the sequence:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377……..
I like the following representation:
Robert Simpson’s observation (1753) is:
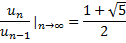
As we go further and further in the sequence, the ratio of two successive terms gets closer and closer to the Golden Ratio.
Fibonacci numbers show up often in nature. For example: the number of petals on a flower, or the number of scales on a pineapple or a pinecone are most often Fibonacci numbers. In the case of the pineapple you’ll note that the scales are in the form of two interlocking spirals. These spirals contain consecutive fibonacci numbers of scales. An implication of this is that the features we see in nature are not entirely coded in the DNA, but rather the DNA codes for processes, which are constrained such that the Fibonacci numbers appear as solutions due to the constraints. Constraints, such as closest packing and the dynamics of growth, could force such a preponderance of Fibonacci numbers.
These numbers were all a result of beginning with the seeds: 1, 1, and then applying the formula, where each element in the series is the sum of the last two elements. What happens if you start with a different seed? What happens when you change the formula?
Quick Science & Math References
- Our Solar System.
- Earth Facts.
- The Metric System.
- Trigonometric Identities.
- Vector & Tensor Identities.
- Explicit Forms of Vector Operators
- Light & Electromagnetic Spectrum.
- Common Laser Wavelengths.
- Human Physiology Facts.
- Human History Timeline
- Geologic Timeline
- Cambrian Explosion
- Life on Earth Timeline
- ASCII Codes and HTML Display Codes
- Thousands of HTML Symbol Codes
- HTML Symbol Codes for Greek Letters
- The Best Way to put Equations on your Web Page
Physics Basics Series
- Basics of Classical Mechanics.
- Basics of Quantum Mechanics.
- Basics of Electrodynamics.
- Basics of Optics.
- Basics of Mathematical Tools for Physics.
- Basics of Plasma Physics.
- Basics of Solid State Physics.
Math Basics Series
- Numbers
- Arithmetic
- Algebra
- Geometry
- Analysis
Technology Basics Series
- Basics of Remote Sensing.
- Basics of Digital Signal Processing.
- Critical Electronic Circuits
- Infrared Imaging Basics
Knowledge Branches
- Information Theory
- How Reading Works in the Brain
- Psychology of Learning
- Logic
WORK IN PROGRESS
- What is the Stark Effect?
- The Chemistry of Love &/or Addiction
- Critical Thinking: How to question what you see, read or hear.
- Aristotle's Prior Analytics - the birth of Logic.
- Optical Solutions, lenses that solve problems
- Fractals
- PTC - Photon Transfer Curve or Mean Variance Analysis
- 3-D Noise
- Laser Primer
- Rail Guns
- Special Relativity
- Radar Technology
- Acousto-optic Cells
- Harmonic Generation for Laser Frequency Doubling (SHG) and Tripling -using non-linear crystals.
- Measurement: Accuracy & Precision.
- Things you should know about computer modeling of physical phenomena!
- Giant Magneto-resistance
- Peltier Cooling
- Pyro-Electric Detectors
- Piezo-Electric Crystals
- Laser Speckle
- FFT and DFT the fast fourier transform and the discrete fourier transform
- Fabry Perot Etalon
- The Hydrogen Atom.
- PCA (Principal Component Analysis)
- Energy per mass in fuels such as Hydrogen, Gasoline, Kerosene, HMX etc...
- Nobel prize winning work on the CCD
- How does a CCD work and what are the normal characteristics of a CCD
- Nobel Prize Winning work on Giant Magneto-resistance
- FROG -frequency resolved optical gating
- Optical Wavefront Sensing
- THz imaging and time-domain spectroscopy
- Camera Calibration
- Laser Designators
- Resampling